1 results
Counting processes with Bernštein intertimes and random jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1028-1044
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
-
In this paper we consider point processes Nf (t), t > 0, with independent increments and integer-valued jumps whose distribution is expressed in terms of Bernštein functions f with Lévy measure v. We obtain the general expression of the probability generating functions Gf of Nf, the equations governing the state probabilities pkf of Nf, and their corresponding explicit forms. We also give the distribution of the first-passage times Tkf of Nf, and the related governing equation. We study in detail the cases of the fractional Poisson process, the relativistic Poisson process, and the gamma-Poisson process whose state probabilities have the form of a negative binomial. The distribution of the times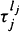
of jumps with height lj (
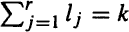) under the condition N(t) = k for all these special processes is investigated in detail.
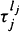of jumps with height 
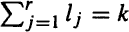) under the condition 