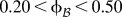1 results
Skeletonization-based beam finite element models for stochastic bicontinuous materials: Application to simulations of nanoporous gold
-
- Journal:
- Journal of Materials Research / Volume 33 / Issue 20 / 29 October 2018
- Published online by Cambridge University Press:
- 27 July 2018, pp. 3371-3382
- Print publication:
- 29 October 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
An efficient representative volume element generation strategy is developed in modeling nanoporous materials. It uses periodic 3D beam finite element (FE) models derived from skeletonization of spinodal-like stochastic microstructures produced by a leveled random field. To mimic stiffening with agglomeration of the mass at junctions, an increased Young’s modulus is assigned to the elements within the junction zone. The effective Young’s modulus, Poisson’s ratio, and universal anisotropy index are computed. A good agreement of the Young’s modulus predictions with those obtained from experimental results for phase volume fractions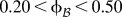
$0.20 \lt {\phi _{\cal B}} \lt 0.50$ is observed. Moreover, the elastic anisotropy index of the generated beam networks shows sufficient proximity to isotropy. Finally, it is demonstrated that, as compared to the simulation statistics of voxel-FE models, for the beam-FE models over 500-fold computational acceleration with 250-fold less memory requirement is provided.
