1 results
On bar lengths in partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 535-550
-
- Article
-
- You have access
- Export citation
-
We present, given an odd integer d, a decomposition of the multiset of bar lengths of a bar partition λ as the union of two multisets, one consisting of the bar lengths in its d-core partition cd(λ) and the other consisting of modified bar lengths in its d-quotient partition. In particular, we obtain that the multiset of bar lengths in cd(λ) is a sub-multiset of the multiset of bar lengths in λ. Also, we obtain a relative bar formula for the degrees of spin characters of the Schur extensions of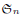
. The proof involves a recent similar result for partitions, proved by Bessenrodt and the authors.
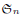. The proof involves a recent similar result for partitions, proved by Bessenrodt and the authors.