We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For an analytic function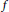 
$f$ on the unit disk 
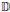$\mathbb{D}$, we show that the 
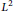${{L}^{2}}$ integral mean of 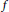$f$ on 
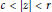$\text{c}\,\text{}\,\text{ }\!\!|\!\!\text{ z }\!\!|\!\!\text{ }\,\text{}\,\text{r}$ with respect to the weighted area measure 
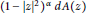${{\left( 1\,-\,|z{{|}^{2}} \right)}^{\alpha }}dA\left( z \right)$ is a logarithmically convex function of 
$r$ on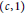 
$\left( c,\,1 \right)$, where 
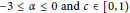$-3\,\le \,\alpha \,\le \,0\,\text{and}\,\text{c}\,\in \,[\,0,\,1)$. Moreover, the range 
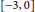$[-3,\,0]$ for 
$\alpha $ is best possible. When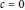 
$c\,=\,0$, our arguments here also simplify the proof for several results we obtained in earlier papers.
