Let 𝔻 be the open unit disc, let v:𝔻→(0,∞) be a typical weight, and let Hv∞ be the corresponding weighted Banach space consisting of analytic functions f on 𝔻 such that 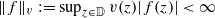 . We call Hv∞ a typical-growth space. For ϕ a holomorphic self-map of 𝔻, let Cφ denote the composition operator induced by ϕ. We say that Cφ is a bellwether for boundedness of composition operators on typical-growth spaces if for each typical weight v, Cφ acts boundedly on Hv∞ only if all composition operators act boundedly on Hv∞. We show that a sufficient condition for Cφ to be a bellwether for boundedness is that ϕ have an angular derivative of modulus less than 1 at a point on ∂𝔻. We raise the question of whether this angular-derivative condition is also necessary for Cφ to be a bellwether for boundedness.
. We call Hv∞ a typical-growth space. For ϕ a holomorphic self-map of 𝔻, let Cφ denote the composition operator induced by ϕ. We say that Cφ is a bellwether for boundedness of composition operators on typical-growth spaces if for each typical weight v, Cφ acts boundedly on Hv∞ only if all composition operators act boundedly on Hv∞. We show that a sufficient condition for Cφ to be a bellwether for boundedness is that ϕ have an angular derivative of modulus less than 1 at a point on ∂𝔻. We raise the question of whether this angular-derivative condition is also necessary for Cφ to be a bellwether for boundedness.

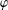
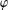
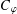
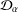
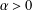
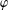
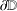
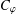
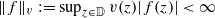 . We call
. We call 