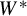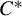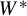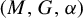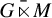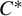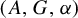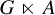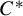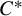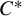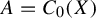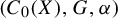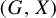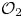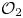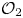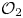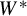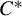We establish several new characterizations of amenable $W^*$ - and $C^*$ -dynamical systems over arbitrary locally compact groups. In the 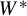$W^*$ -setting we show that amenability is equivalent to (1) a Reiter property and (2) the existence of a certain net of completely positive Herz–Schur multipliers of 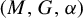$(M,G,\alpha )$ converging point weak* to the identity of 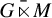$G\bar {\ltimes }M$ . In the 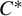$C^*$ -setting, we prove that amenability of 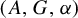$(A,G,\alpha )$ is equivalent to an analogous Herz–Schur multiplier approximation of the identity of the reduced crossed product 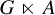$G\ltimes A$ , as well as a particular case of the positive weak approximation property of Bédos and Conti [On discrete twisted 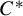$C^*$ -dynamical systems, Hilbert 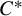$C^*$ -modules and regularity. Münster J. Math.5 (2012), 183–208] (generalized to the locally compact setting). When $Z(A^{**})=Z(A)^{**}$ , it follows that amenability is equivalent to the 1-positive approximation property of Exel and Ng [Approximation property of 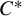$C^*$ -algebraic bundles. Math. Proc. Cambridge Philos. Soc.132(3) (2002), 509–522]. In particular, when 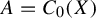$A=C_0(X)$ is commutative, amenability of 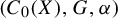$(C_0(X),G,\alpha )$ coincides with topological amenability of the G-space 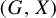$(G,X)$ .

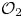We show that, up to strong cocycle conjugacy, every countable exact group admits a unique equivariantly $\mathcal {O}_{2}$-absorbing, pointwise outer action on the Cuntz algebra $\mathcal {O}_{2}$ with the quasi-central approximation property (QAP). In particular, we establish the equivariant analogue of the Kirchberg $\mathcal {O}_{2}$-absorption theorem for these groups.