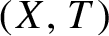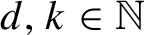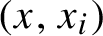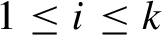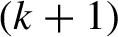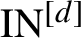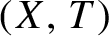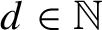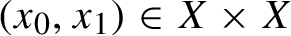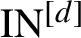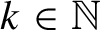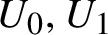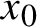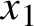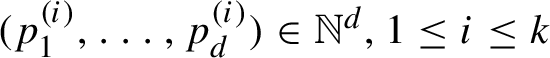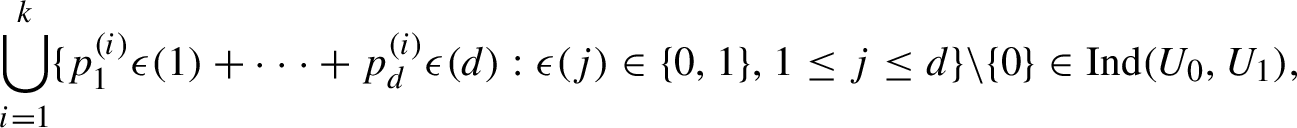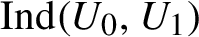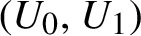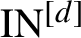In this paper it is shown that for a minimal system
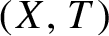 $(X,T)$
and
$(X,T)$
and
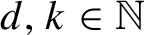 $d,k\in \mathbb {N}$
, if
$d,k\in \mathbb {N}$
, if
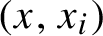 $(x,x_{i})$
is regionally proximal of order d for
$(x,x_{i})$
is regionally proximal of order d for
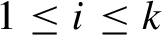 $1\leq i\leq k$
, then
$1\leq i\leq k$
, then
 $(x,x_{1},\ldots ,x_{k})$
is
$(x,x_{1},\ldots ,x_{k})$
is
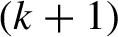 $(k+1)$
-regionally proximal of order d. Meanwhile, we introduce the notion of
$(k+1)$
-regionally proximal of order d. Meanwhile, we introduce the notion of
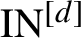 $\mathrm {IN}^{[d]}$
-pair: for a dynamical system
$\mathrm {IN}^{[d]}$
-pair: for a dynamical system
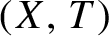 $(X,T)$
and
$(X,T)$
and
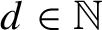 $d\in \mathbb {N}$
, a pair
$d\in \mathbb {N}$
, a pair
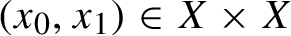 $(x_{0},x_{1})\in X\times X$
is called an
$(x_{0},x_{1})\in X\times X$
is called an
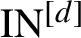 $\mathrm {IN}^{[d]}$
-pair if for any
$\mathrm {IN}^{[d]}$
-pair if for any
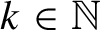 $k\in \mathbb {N}$
and any neighborhoods
$k\in \mathbb {N}$
and any neighborhoods
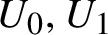 $U_{0} ,U_{1} $
of
$U_{0} ,U_{1} $
of
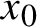 $x_{0}$
and
$x_{0}$
and
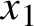 $x_{1}$
respectively, there exist different
$x_{1}$
respectively, there exist different
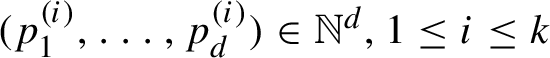 $(p_{1}^{(i)},\ldots ,p_{d}^{(i)})\in \mathbb {N}^{d} , 1\leq i\leq k$
, such that
$(p_{1}^{(i)},\ldots ,p_{d}^{(i)})\in \mathbb {N}^{d} , 1\leq i\leq k$
, such that
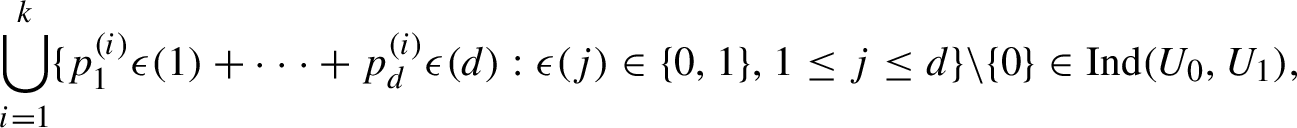 $$ \begin{align*} \bigcup_{i=1}^{k}\{ p_{1}^{(i)}\epsilon(1)+\cdots+p_{d}^{(i)} \epsilon(d):\epsilon(j)\in \{0,1\},1\leq j\leq d\}\backslash \{0\}\in \mathrm{Ind}(U_{0},U_{1}), \end{align*} $$
$$ \begin{align*} \bigcup_{i=1}^{k}\{ p_{1}^{(i)}\epsilon(1)+\cdots+p_{d}^{(i)} \epsilon(d):\epsilon(j)\in \{0,1\},1\leq j\leq d\}\backslash \{0\}\in \mathrm{Ind}(U_{0},U_{1}), \end{align*} $$
where
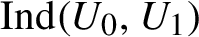 $\mathrm {Ind}(U_{0},U_{1})$
denotes the collection of all independence sets for
$\mathrm {Ind}(U_{0},U_{1})$
denotes the collection of all independence sets for
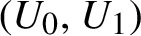 $(U_{0},U_{1})$
. It turns out that for a minimal system, if it does not contain any non-trivial
$(U_{0},U_{1})$
. It turns out that for a minimal system, if it does not contain any non-trivial
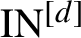 $\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d.
$\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d.