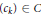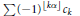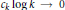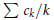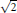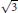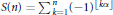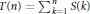1 results
On the Convergence of a Class of Nearly Alternating Series
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 1 / 01 February 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 85-108
- Print publication:
- 01 February 2007
-
- Article
-
- You have access
- Export citation
-
Let
$C$ be the class of convex sequences of real numbers. The quadratic irrational numbers can be partitioned into two types as follows. If 
$\alpha$ is of the first type and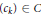 
$\left( {{c}_{k}} \right)\,\in C$, then 
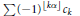$\sum{{{(-1)}^{\left\lfloor k\alpha \right\rfloor }}}{{c}_{k}}$ converges if and only if 
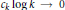${{c}_{k}}\log k\to 0$.
If $\alpha$ is of the second type and 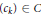$\left( {{c}_{k}} \right)\,\in C$, then 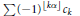$\sum{{{(-1)}^{\left\lfloor k\alpha \right\rfloor }}}{{c}_{k}}$ converges if and only if 
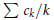$\sum{{{c}_{k}}/k}$ converges. An example of a quadratic irrational of the first type is 
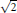$\sqrt{2}$, and an example of the second type is 
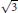$\sqrt{3}$. The analysis of this problem relies heavily on the representation of $\alpha$ as a simple continued fraction and on properties of the sequences of partial sums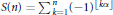 
$S\left( n \right)\,=\,{{\sum\nolimits_{k=1}^{n}{\left( -1 \right)}}^{\left\lfloor k\alpha \right\rfloor }}$ and double partial sums 
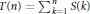$T\left( n \right)\,=\,\sum\nolimits_{k=1}^{n}{\,S\left( k \right)}$.
