We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we study Zimmer's conjecture for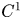 
$C^{1}$ actions of lattice subgroup of a higher-rank simple Lie group with finite center on compact manifolds. We show that when the rank of an uniform lattice is larger than the dimension of the manifold, then the action factors through a finite group. For lattices in 
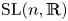${\rm SL}(n, {{\mathbb {R}}})$, the dimensional bound is sharp.
