Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

weil-petersson volumes

Journal of the Institute of Mathematics of Jussieu (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

THE SIMPLE SEPARATING SYSTOLE FOR HYPERBOLIC SURFACES OF LARGE GENUS
Part of
- Low-dimensional topology
- Deformations of analytic structures
Hugo Parlier, Yunhui Wu, Yuhao Xue
Journal:

Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022

Published online by Cambridge University Press:

31 May 2021, pp. 2205-2214

Print publication:

November 2022
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
In this note we show that the expected value of the separating systole of a random surface of genus g with respect to Weil–Petersson volume behaves like 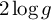$2\log g $ as the genus goes to infinity. This is in strong contrast to the behavior of the expected value of the systole which, by results of Mirzakhani and Petri, is independent of genus.