Search

When is an ideal of a ring radical or prime? By examining its generators, one may in many cases definably and uniformly test the ideal’s properties. We seek to establish such definable formulas in rings of p-adic power series, such as 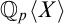$\mathbb Q_{p}\langle X\rangle $ , 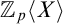$\mathbb Z_{p}\langle X\rangle $ , and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.