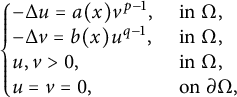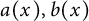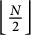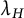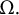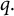In this paper, we are interested in positive solutions of 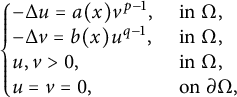 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align*} $$ $\Omega $ is a bounded annular domain (not necessarily an annulus) in
$\Omega $ is a bounded annular domain (not necessarily an annulus) in  ${\mathbb {R}}^N (N \ge 3)$ and
${\mathbb {R}}^N (N \ge 3)$ and 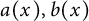 $ a(x), b(x)$ are positive continuous functions. We show the existence of a positive solution for a range of supercritical values of p and q when the problem enjoys certain mild symmetry and monotonicity conditions. We shall also address the symmetry breaking phenomena where the system is fully symmetric. Indeed, as a consequence of our results, we shall show that problem (1) has
$ a(x), b(x)$ are positive continuous functions. We show the existence of a positive solution for a range of supercritical values of p and q when the problem enjoys certain mild symmetry and monotonicity conditions. We shall also address the symmetry breaking phenomena where the system is fully symmetric. Indeed, as a consequence of our results, we shall show that problem (1) has 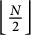 $\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $ (the floor of
$\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $ (the floor of  $\frac {N}{2}$) positive non-radial solutions when
$\frac {N}{2}$) positive non-radial solutions when  $ a(x)=b(x)=1$ and
$ a(x)=b(x)=1$ and  $\Omega $ is an annulus with certain assumptions on the radii. In general, for the radial case where the domain is an annulus, we prove the existence of a non-radial solution provided
$\Omega $ is an annulus with certain assumptions on the radii. In general, for the radial case where the domain is an annulus, we prove the existence of a non-radial solution provided  $$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$
$$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$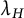 $\lambda _H$ is the best constant for the Hardy inequality on
$\lambda _H$ is the best constant for the Hardy inequality on 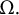 $\Omega .$ We remark that the best constant
$\Omega .$ We remark that the best constant  $\lambda _H$ for the Hardy inequality is just the characteristic of the domain, and is independent of the choices of p and
$\lambda _H$ for the Hardy inequality is just the characteristic of the domain, and is independent of the choices of p and 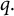 $q.$ For this reason, the aforementioned inequality plays a major role to prove the existence and multiplicity of non-radial solutions when the problem is fully symmetric. Our proofs use a variational formulation on appropriate convex subsets for which the lack of compactness is recovered for the supercritical problem.
$q.$ For this reason, the aforementioned inequality plays a major role to prove the existence and multiplicity of non-radial solutions when the problem is fully symmetric. Our proofs use a variational formulation on appropriate convex subsets for which the lack of compactness is recovered for the supercritical problem.