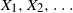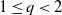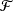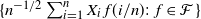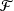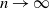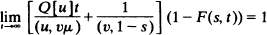Let $X_1, X_2,\dots$ be a short-memory linear process of random variables. For $1\leq q<2$ , let ${\mathcal{F}}$ be a bounded set of real-valued functions on [0, 1] with finite q-variation. It is proved that $\{n^{-1/2}\sum_{i=1}^nX_i\,f(i/n)\colon f\in{\mathcal{F}}\}$ converges in outer distribution in the Banach space of bounded functions on ${\mathcal{F}}$ as $n\to\infty$ . Several applications to a regression model and a multiple change point model are given.

Let Z(t) ··· (Z1(t), …, Zk (t)) be an indecomposable critical k-type age-dependent branching process with generating function F(s, t). Denote the right and left eigenvalues of the mean matrix M by u and v respectively and suppose μ is the vector of mean lifetimes, i.e. Mu = u, vM = v.

It is shown that, under second moment assumptions, 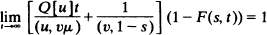uniformly for s ∈ ([0, 1]k of the form s = 1 – cu, c a constant. Here vμ is the componentwise product of the vectors and Q[u] is a constant.

This result is then used to give a new proof of the exponential limit law.