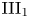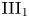1 results
Haagerup and Størmer's conjecture on pointwise inner automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 2480-2495
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
In 1988, Haagerup and Størmer conjectured that every pointwise inner automorphism of a type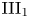
${\rm III_1}$ factor is a composition of an inner and a modular automorphism. We study this conjecture and prove that every type 
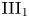${\rm III_1}$ factor with trivial bicentralizer indeed satisfies this condition. In particular, this shows that Haagerup and Størmer's conjecture holds in full generality if Connes’ bicentralizer problem has an affirmative answer. Our proof is based on Popa's intertwining theory and Marrakchi's recent work on relative bicentralizers.
