1 results
A threshold AR(1) model
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 270-286
- Print publication:
- June 1984
-
- Article
- Export citation
-
We consider the model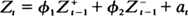
where φ1, φ2 are real coefficients, not necessarily equal, and the at,'s are a sequence of i.i.d. random variables with mean 0. Necessary and sufficient conditions on the φ 's are given for stationarity of the process. Least squares estimators of the φ 's are derived and, under mild regularity conditions, are shown to be consistent and asymptotically normal. An hypothesis test is given to differentiate between an AR(1) (the case φ1 = φ2) and this threshold model. The asymptotic behavior of the test statistic is derived. Small-sample behavior of the estimators and the hypothesis test are studied via simulated data.
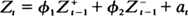where 