We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A new oscillation criterion is given for general superlinear ordinary differential equations of second order of the form x″(t)+ a(t)f[x(t)]=0, where a ∈ C([t0∞,)), f∈C(R) with yf(y)>0 for y≠0 and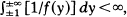 
and f is continously differentiable on R-{0} with f'(y)≥0 for all y≠O. In the special case of the differential equation 
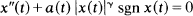(γ > 1) this criterion leads to an oscillation result due to Wong [9].
