This paper describes the limiting asymptotic behaviour of a long cascade of linear reservoirs fed by stationary inflows into the first reservoir. We show that the storage in the nth reservoir becomes asymptotically deterministic as n → ∞, and establish a central limit theorem for the random fluctuations about the deterministic approximation. In addition, we prove a large deviations theorem that provides precise logarithmic asymptotics for the tail probabilities associated with the storage in the nth reservoir when n is large.

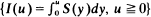 where
where 