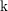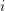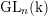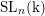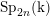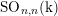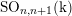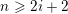For a field $\text{k}$, we prove that the $i$th homology of the groups $\operatorname{GL}_{n}(\text{k})$, $\operatorname{SL}_{n}(\text{k})$, $\operatorname{Sp}_{2n}(\text{k})$, $\operatorname{SO}_{n,n}(\text{k})$, and $\operatorname{SO}_{n,n+1}(\text{k})$ with coefficients in their Steinberg representations vanish for $n\geqslant 2i+2$.

Dedicated to the memory of Professor A. I. Kostrikin

The main problem under discussion is to determine, for quasi-simple groups of Lie type G, irreducible representations $\phi$ of G that remain irreducible under reduction modulo the natural prime p. The method is new. It works only for p >3 and for representations $\phi$ that can be realized over an unramified extension of ${\mathbb Q}_p$, the field of p -adic numbers. Under these assumptions, the main result says that the trivial and the Steinberg representations of G are the only representations in question provided G is not of type A1. This is not true for G=SL(2, p). The paper contains a result of independent interest on infinitesimally irrreducible representations $\rho$ of G over an algebraically closed field of characteristic p. Assuming that G is not of rank 1 and $G\neq G_2(5)$, it is proved that either the Jordan normal form of a root element contains a block of size d with 1<d<p -1 or the highest weight of $\rho$ is equal to p -1 times the sum of the fundamental weights.

2000 Mathematical Subject Classification: 20C33, 20G15.