We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We apply results from both contact topology and exceptional surgery theory to study when Legendrian surgery on a knot yields a reducible manifold. As an application, we show that a reducible surgery on a non-cabled positive knot of genus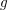 
$g$ must have slope 
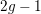$2g-1$, leading to a proof of the cabling conjecture for positive knots of genus 2. Our techniques also produce bounds on the maximum Thurston–Bennequin numbers of cables.
