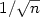We consider a diffusion process X which is observed at times i/nfor i = 0,1,...,n, each observation being subject to a measurementerror. All errors are independent and centered Gaussian with knownvariance pn . There is an unknown parameter to estimate within thediffusion coefficient. In this second paper weconstruct estimators which are asymptotically optimal when theprocess X is a Gaussian martingale, and we conjecture that they arealso optimal in the general case.

We consider a diffusion process X which is observed at times i/nfor i = 0,1,...,n, each observation being subject to a measurementerror. All errors are independent and centered Gaussian with knownvariance pn . There is an unknown parameter within the diffusioncoefficient, to be estimated. In this first paper thecase when X is indeed a Gaussian martingale is examined: we can provethat the LAN property holds under quite weak smoothness assumptions,with an explicit limiting Fisher information. What is perhaps the mostinteresting is the rate at which this convergence takes place:it is $1/\sqrt{n}$ 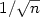(as when there is no measurement error) when pn goes fastenough to 0, namely npn is bounded. Otherwise, and provided thesequence pn itself is bounded, the rate is (pn / n) 1/4. Inparticular if pn = p does not depend on n, we get a rate n -1/4.