In the following note, we focus on the problem of existence of continuous solutions vanishing at infinity to the equation div v = f for f ∈ Ln(ℝn) and satisfying an estimate of the type ||v||∞ ⩽ C||f||n for any f ∈ Ln(ℝn), where C > 0 is related to the constant appearing in the Sobolev–Gagliardo–Nirenberg inequality for functions with bounded variation (BV functions).
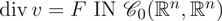 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$