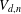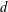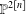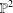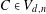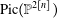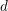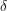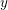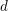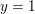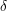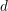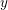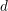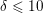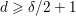The Severi variety $V_{d,n}$ of plane curves of a given degree $d$ and exactly $n$ nodes admits a map to the Hilbert scheme $\mathbb{P}^{2[n]}$ of zero-dimensional subschemes of $\mathbb{P}^{2}$ of degree $n$. This map assigns to every curve $C\in V_{d,n}$ its nodes. For some $n$, we consider the image under this map of many known divisors of the Severi variety and its partial compactification. We compute the divisor classes of such images in $\text{Pic}(\mathbb{P}^{2[n]})$ and provide enumerative numbers of nodal curves. We also answer directly a question of Diaz–Harris [‘Geometry of the Severi variety’, Trans. Amer. Math. Soc.309 (1988), 1–34] about whether the canonical class of the Severi variety is effective.

The Severi degree is the degree of the Severi variety parametrizing plane curves of degree 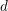$d$ with 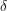${\it\delta}$ nodes. Recently, Göttsche and Shende gave two refinements of Severi degrees, polynomials in a variable 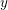$y$, which are conjecturally equal, for large 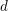$d$. At 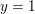$y=1$, one of the refinements, the relative Severi degree, specializes to the (non-relative) Severi degree. We give a tropical description of the refined Severi degrees, in terms of a refined tropical curve count for all toric surfaces. We also refine the equivalent count of floor diagrams for Hirzebruch and rational ruled surfaces. Our description implies that, for fixed 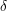${\it\delta}$, the refined Severi degrees are polynomials in 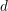$d$ and 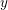$y$, for large 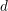$d$. As a consequence, we show that, for 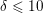${\it\delta}\leqslant 10$ and all 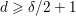$d\geqslant {\it\delta}/2+1$, both refinements of Göttsche and Shende agree and equal our refined counts of tropical curves and floor diagrams.

We give a full description of the Chow ring of the complex Cayley plane $\mathbb{O}\mathbb{P}^2$. For this, we describe explicitly the most interesting of its Schubert varieties and compute their intersection products. Translating our results into the Borel presentation, i.e. in terms of Weyl group invariants, we are able to compute the degree of the variety of reductions Y8 introduced by the current authors in arXiv: math.AG/0306328.

Let S be a smooth, minimal rational surface. The geometry of the Severi variety parametrising irreducible, rational curves in a given linear system on S is studied. The results obtained are applied to enumerative geometry, in combination with ideas from Quantum Cohomology. Formulas enumerating rational curves are found, some of which generalised Kontsevich‘s formula for plane curves.