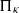Characterization of generalized Schur functions in terms of their Taylor coefficients was established by Krein and Langer [‘Über einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume ${\Pi }_{\kappa } $ zusammenhängen. I. Einige Funktionenklassen und ihre Darstellungen’, Math. Nachr. 77 (1977), 187–236]. We establish a boundary analogue of this characterization.

Given a sequence $\{A_n\}_{n\in\mathbb{Z}_+}$ of bounded linear operators between complex Hilbert spaces $\mathcal{H}$ and $\mathcal{K}$ we characterize the existence of a contraction (resp. isometry, unitary operator, shift) $T$ on $\mathcal{K}$ such that \[A_n=T^nA_0,\quad n\in\mathbb{Z}_+.\] Such moment problems are motivated by their connection with the dilatability of positive operator measures having applications in the theory of stochastic processes.

The solutions, based on the fact that a certain operator function attached to $T$ is positive definite on $\mathbb{Z}$, extend the ones given by Sebestyén in [18], [19] or, recently, by Jabłoński and Stochel in [8]. Some applications, containing new characterizations for isometric, unitary operators, orthogonal projections or commuting pairs having regular dilation, conclude the paper.