It is a question of Arhangel'skiĭ [1] (Problem 2) whether the identity ψ(G) = X(G) holds for every minimal Hausdorff topological group G = 〈G,u〉). (Here, as usual, ψ(G), the pseudocharacter of G, is the least cardinal number K for which there is 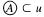 such that
such that 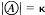 and
and 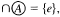 and x(G), the character of G,is the least cardinality of a local base at e for (〈G,u〉.) That 〈G, u〉 is minimal means that, if v is a Hausdorff topological group topology for G and v ⊂ u, then v = u.
and x(G), the character of G,is the least cardinality of a local base at e for (〈G,u〉.) That 〈G, u〉 is minimal means that, if v is a Hausdorff topological group topology for G and v ⊂ u, then v = u.
In this paper, we give some conditions on G sufficient to ensure a positive response to Arhangel'skiï's question, and we offer an example which responds negatively to a question on minimal groups posed some years ago (cf. [6] (p. 107) and [4] (p. 259)).
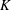 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES