We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For a derivation δ of a commutative Noetherian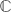 
${\mathbb C}$-algebra A, a homeomorphism is established between the prime spectrum of the Ore extension A[z;δ] and the Poisson prime spectrum of the polynomial algebra A[z] endowed with the Poisson bracket such that {A,A}=0 and {z,a}=δ(a) for all a ∈ A.
