We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A subgroup A of a group G is said to be hereditarily G-permutable with a subgroup B of G, if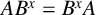 
$AB^x = B^xA$ for some element 
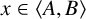$x \in \langle A, B \rangle $. A subgroup A of a group G is said to be hereditarily G-permutable in G if A is hereditarily G-permutable with every subgroup of G. In this paper, we investigate the structure of a finite group G with all its Schmidt subgroups hereditarily G-permutable.
