1 results
On the Structure of the Schild Group in Relativity Theory
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 774-790
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
-
Alfred Schild has established conditions that Lorentz transformationsmap world-vectors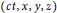
$(ct,x,y,z)$ with integer coordinates onto vectors of the same kind. These transformations are called integral Lorentz transformations.This paper contains supplements to our earlier work with a new focus on group theory. To relate the results to the familiar matrix group nomenclature, we associate Lorentz transformations with matrices in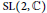
$\text{SL}(2,\mathbb{C})$. We consider the lattice of subgroups of the group originated in Schild's paper and obtain generating sets for the full group and its subgroups.
