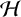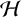1 results
ON SEPARABILITY FINITENESS CONDITIONS IN SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 402-430
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Taking residual finiteness as a starting point, we consider three related finiteness properties: weak subsemigroup separability, strong subsemigroup separability and complete separability. We investigate whether each of these properties is inherited by Schützenberger groups. The main result of this paper states that for a finitely generated commutative semigroup S, these three separability conditions coincide and are equivalent to every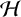
$\mathcal {H}$
-class of S being finite. We also provide examples to show that these properties in general differ for commutative semigroups and finitely generated semigroups. For a semigroup with finitely many 
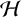$\mathcal {H}$
-classes, we investigate whether it has one of these properties if and only if all its Schützenberger groups have the property.
