We give a unified presentation of stability results for stochastic vector difference equations 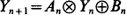 based on various choices of binary operations
based on various choices of binary operations 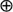 and
and 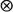 , assuming that
, assuming that 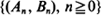 are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is E[log |A0|] < 0. In the generalizations, the condition takes the form γ< 0, where γis the limit of a subadditive process associated with
are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is E[log |A0|] < 0. In the generalizations, the condition takes the form γ< 0, where γis the limit of a subadditive process associated with 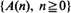 . Under this and mild additional conditions, the process
. Under this and mild additional conditions, the process 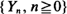 has a unique finite stationary distribution to which it converges from all initial conditions.
has a unique finite stationary distribution to which it converges from all initial conditions.
The variants of standard matrix algebra we consider replace the operations + and × with (max, +), (max,×), (min, +), or (min,×). In each case, the appropriate stability condition parallels that for the standard recursions, involving certain subadditive limits. Since these limits are difficult to evaluate, we provide bounds, thus giving alternative, computable conditions for stability.

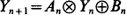 based on various choices of binary operations
based on various choices of binary operations 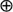 and
and 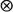 , assuming that
, assuming that 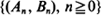 are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is
are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is 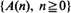 . Under this and mild additional conditions, the process
. Under this and mild additional conditions, the process 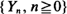 has a unique finite stationary distribution to which it converges from all initial conditions.
has a unique finite stationary distribution to which it converges from all initial conditions.