Infinitely many new Einstein Finsler metrics are constructed on several homogeneous spaces. By imposing certain conditions on the homogeneous spaces, it is shown that the Ricci constant condition becomes an ordinary differential equation. The regular solutions of this equation lead to a two parameter family of Einstein Finsler metrics with vanishing 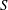 $S$ curvature.
$S$ curvature.
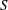 $S$ Curvature
$S$ Curvature