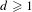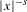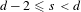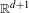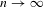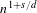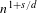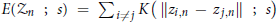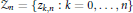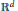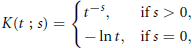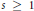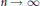We study systems of $n$ points in the Euclidean space of dimension $d\geqslant 1$ interacting via a Riesz kernel $|x|^{-s}$ and confined by an external potential, in the regime where $d-2\leqslant s<d$. We also treat the case of logarithmic interactions in dimensions 1 and 2. Our study includes and retrieves all cases previously studied in Sandier and Serfaty [2D Coulomb gases and the renormalized energy, Ann. Probab. (to appear); 1D log gases and the renormalized energy: crystallization at vanishing temperature (2013)] and Rougerie and Serfaty [Higher dimensional Coulomb gases and renormalized energy functionals, Comm. Pure Appl. Math. (to appear)]. Our approach is based on the Caffarelli–Silvestre extension formula, which allows one to view the Riesz kernel as the kernel of an (inhomogeneous) local operator in the extended space $\mathbb{R}^{d+1}$.

As $n\rightarrow \infty$, we exhibit a next to leading order term in $n^{1+s/d}$ in the asymptotic expansion of the total energy of the system, where the constant term in factor of $n^{1+s/d}$ depends on the microscopic arrangement of the points and is expressed in terms of a ‘renormalized energy’. This new object is expected to penalize the disorder of an infinite set of points in whole space, and to be minimized by Bravais lattice (or crystalline) configurations. We give applications to the statistical mechanics in the case where temperature is added to the system, and identify an expected ‘crystallization regime’. We also obtain a result of separation of the points for minimizers of the energy.

We consider the $s$-energy 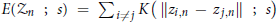$E({{Z}_{n}};\,s)={{\Sigma }_{i\ne j}}K(\parallel {{z}_{i,n}}\,-\,{{z}_{j,n}}\parallel \,;\,s)$ for point sets 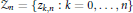$Zn\,=\,\{{{z}_{k,n}}\,:\,k\,=\,0,\,\ldots \,,\,n\} $ on certain compact sets $\Gamma $ in 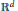${{\mathbb{R}}^{d}}$ having finite one-dimensional Hausdorff measure,where

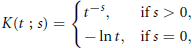$$K(t;\,s)\,=\,\left\{ _{-\ln \,t,\,\,\,\text{if}\,s\,=\,0,\,}^{{{t}^{-s}},\,\,\,\,\,\,\,\text{if}\,s\,>\,0,} \right\}$$

is the Riesz kernel. Asymptotics for the minimum $s$-energy and the distribution of minimizing sequences of points is studied. In particular, we prove that, for 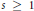$s\,\ge \,1$, the minimizing nodes for a rectifiable Jordan curve Γ distribute asymptotically uniformly with respect to arclength as 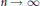$n\,\to \,\infty $.