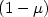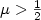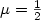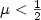In the present paper, we consider a wave system that is fixed at one end and a boundary control input possessing a partial time delay of weight $(1-\mu)$ 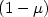is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop systemgenerates a C 0 group of linear operators. After a spectral analysis, we show that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors andgeneralized eigenvectors that forms a Riesz basis for the state Hilbert space.Furthermore, we show that when the weight $\mu>\frac{1}{2}$ 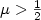, for any time delay,we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When $\mu=\frac{1}{2}$ 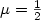, we show that the system is at most asymptotically stable. When $\mu<\frac{1}{2}$ 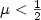, the system is always unstable.

We intend to conduct a fairly complete study on Timoshenko beams with pointwise feedback controls and seek to obtain information about the eigenvalues, eigenfunctions, Riesz-Basis-Property, spectrum-determined-growth-condition, energy decay rate and various stabilities for the beams. One major difficulty of the present problem is the non-simplicity of the eigenvalues. In fact, we shall indicate in this paper situations where the multiplicity of the eigenvalues is at least two. We build all the above-mentioned results from an effective asymptotic analysis on both the eigenvalues and the eigenfunctions, and conclude with the Riesz-Basis-Property and the spectrum-determined-growth-condition. Finally, these results are used to examine the stability effects on the system by the location of the pointwise control relative to the length of the whole beam.

We study the simultaneously reachable subspace for two strings controlled from a common endpoint. We give necessary and sufficient conditions for simultaneous spectral and approximate controllability. Moreover we prove the lack of simultaneous exact controllability and we study the space of simultaneously reachable states as a function of the position of the joint. For each type of controllability result we give the sharp controllability time.