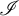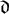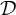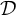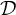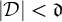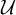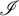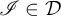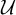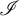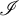We give a new characterization of the cardinal invariant 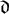 $\mathfrak {d}$ as the minimal cardinality of a family
$\mathfrak {d}$ as the minimal cardinality of a family 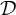 $\mathcal {D}$ of tall summable ideals such that an ultrafilter is rapid if and only if it has non-empty intersection with all the ideals in the family
$\mathcal {D}$ of tall summable ideals such that an ultrafilter is rapid if and only if it has non-empty intersection with all the ideals in the family 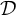 $\mathcal {D}$. On the other hand, we prove that in the Miller model, given any family
$\mathcal {D}$. On the other hand, we prove that in the Miller model, given any family 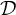 $\mathcal {D}$ of analytic tall p-ideals such that
$\mathcal {D}$ of analytic tall p-ideals such that 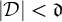 $\vert \mathcal {D}\vert <\mathfrak {d}$, there is an ultrafilter
$\vert \mathcal {D}\vert <\mathfrak {d}$, there is an ultrafilter 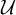 $\mathcal {U}$ which is an
$\mathcal {U}$ which is an 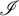 $\mathscr {I}$-ultrafilter for all ideals
$\mathscr {I}$-ultrafilter for all ideals 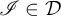 $\mathscr {I}\in \mathcal {D}$ at the same time, yet
$\mathscr {I}\in \mathcal {D}$ at the same time, yet 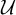 $\mathcal {U}$ is not a rapid ultrafilter. As a corollary, we obtain that in the Miller model, given any analytic tall p-ideal
$\mathcal {U}$ is not a rapid ultrafilter. As a corollary, we obtain that in the Miller model, given any analytic tall p-ideal 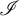 $\mathscr {I}$,
$\mathscr {I}$, 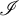 $\mathscr {I}$-ultrafilters are dense in the Rudin–Blass ordering, generalizing a theorem of Bartoszyński and S. Shelah, who proved that in such model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering. This theorem also shows some limitations about possible generalizations of a theorem of C. Laflamme and J. Zhu.
$\mathscr {I}$-ultrafilters are dense in the Rudin–Blass ordering, generalizing a theorem of Bartoszyński and S. Shelah, who proved that in such model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering. This theorem also shows some limitations about possible generalizations of a theorem of C. Laflamme and J. Zhu.
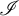 $\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL
$\mathscr {I}$-ULTRAFILTERS IN THE RATIONAL PERFECT SET MODEL