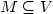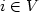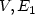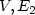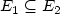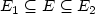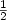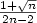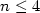A vertex i of a graph G = (V,E) is said to be controlled by $M \subseteq V$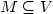 if the majority of the elements of
the neighborhood of i (including itself) belong to M. The set
M is a monopoly in G if every vertex $i\in V$
if the majority of the elements of
the neighborhood of i (including itself) belong to M. The set
M is a monopoly in G if every vertex $i\in V$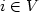 is
controlled by M. Given a set $M \subseteq V$
is
controlled by M. Given a set $M \subseteq V$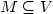 and two graphs
G1 = ($V,E_1$
and two graphs
G1 = ($V,E_1$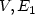 ) and G2 = ($V,E_2$
) and G2 = ($V,E_2$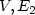 ) where $E_1\subseteq E_2$
) where $E_1\subseteq E_2$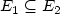 , the
monopoly verification problem (mvp) consists of deciding
whether there exists a sandwich graph G = (V,E) (i.e., a graph
where $E_1\subseteq E\subseteq E_2$
, the
monopoly verification problem (mvp) consists of deciding
whether there exists a sandwich graph G = (V,E) (i.e., a graph
where $E_1\subseteq E\subseteq E_2$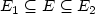 ) such that M is a monopoly
in G = (V,E). If the answer to the mvp is No, we then
consider the max-controlled set problem (mcsp), whose
objective is to find a sandwich graph G = (V,E) such that the
number of vertices of G controlled by M is maximized. The mvp can be solved in polynomial time; the mcsp, however, is
NP-hard. In this work, we present a deterministic polynomial time
approximation algorithm for the mcsp with ratio
$\frac{1}{2}$
) such that M is a monopoly
in G = (V,E). If the answer to the mvp is No, we then
consider the max-controlled set problem (mcsp), whose
objective is to find a sandwich graph G = (V,E) such that the
number of vertices of G controlled by M is maximized. The mvp can be solved in polynomial time; the mcsp, however, is
NP-hard. In this work, we present a deterministic polynomial time
approximation algorithm for the mcsp with ratio
$\frac{1}{2}$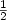 + $\frac{1+\sqrt{n}}{2n-2}$
+ $\frac{1+\sqrt{n}}{2n-2}$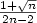 , where n=|V|>4. (The
case $n\leq4$
, where n=|V|>4. (The
case $n\leq4$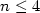 is solved exactly by considering the parameterized
version of the mcsp.) The algorithm is obtained through the
use of randomized rounding and derandomization techniques based on
the method of conditional expectations. Additionally, we show how
to improve this ratio if good estimates of expectation are obtained in advance.
is solved exactly by considering the parameterized
version of the mcsp.) The algorithm is obtained through the
use of randomized rounding and derandomization techniques based on
the method of conditional expectations. Additionally, we show how
to improve this ratio if good estimates of expectation are obtained in advance.