We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Very general forms of the strong law of large numbers and the central limit theorem are proved for estimates of the unknown parameters in a sinusoidal oscillation observed subject to error. In particular when the unknown frequency θ0, is in fact 0 or <it is shown that the estimate,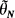 
, satisfies 
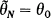for N ≧ N0 (ω) where N0 (ω) is an integer, determined by the realisation, ω, of the process, that is almost surely finite.
