For a fixed k ∈ {1, …, d}, consider arbitrary random vectors X0, …, Xk ∈ ℝd such that the (k + 1)-tuples (UX0, …, UXk) have the same distribution for any rotation U. Let A be any nonsingular d × d matrix. We show that the k-dimensional volume of the convex hull of affinely transformed Xi satisfies 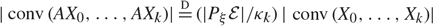\[|{\rm{conv}}(A{X_{\rm{0}}} \ldots ,A{X_k}){\rm{|}}\mathop {\rm{ = }}\limits^{\rm{D}} (|{P_\xi }\varepsilon |/{\kappa _k})|{\rm{conv}}\left( {{X_0}, \ldots ,{X_k}} \right)\], where ɛ:= {x ∈ ℝd : x┬ (A┬A)−1x ≤ 1} is an ellipsoid, Pξ denotes the orthogonal projection to a uniformly chosen random k-dimensional linear subspace ξ independent of X0, …, Xk, and κk is the volume of the unit k-dimensional ball. As an application, we derive the following integral geometry formula for ellipsoids: ck,d,p∫Ad,k |ɛ ∩ E|p+d+1μd,k(dE) = |ɛ|k+1∫Gd,k |PLɛ|pνd,k(dL), where 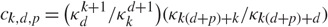$c_{k,d,p} = \big({\kappa_{d}^{k+1}}/{\kappa_k^{d+1}}\big) ({\kappa_{k(d+p)+k}}/{\kappa_{k(d+p)+d}})$. Here p > −1 and Ad,k and Gd,k are the affine and the linear Grassmannians equipped with their respective Haar measures. The p = 0 case reduces to an affine version of the integral formula of Furstenberg and Tzkoni (1971).

Techniques currently available in the literature in dealing with problems in geometric probabilities seem to rely heavily on results from differential and integral geometry. This paper provides a radical departure in this respect. By using purely algebraic procedures and making use of some properties of Jacobians of matrix transformations and functions of matrix argument, the distributional aspects of the random p-content of a p-parallelotope in Euclidean n-space are studied. The common assumptions of independence and rotational invariance of the random points are relaxed and the exact distributions and arbitrary moments, not just integer moments, are derived in this article. General real matrix-variate families of distributions, whose special cases include the mulivariate Gaussian, a multivariate type-1 beta, a multivariate type-2 beta and spherically symmetric distributions, are considered.

It is proved that the r-dimensional volume Vn of the r-simplex spanned by r + 1 sample points taken from the n-fold product distribution of a distribution F is asymptotically normal as n →∞.

Alternative forms of the integral geometric density of an r-subspace [r-flat] containing q[q + 1] points in euclidean n-space Rn are given Stochastic applications in R3 include formulae for

(i) the mean area of intersection of a domain by an isotropic plane through the origin; and

(ii) the variance of the area of intersection of a domain by an isotropic uniform plane.