Let 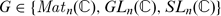 , let
, let 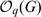 be the quantum function algebra – over
be the quantum function algebra – over 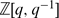 – associated to G, and let
– associated to G, and let 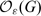 be the specialisation of the latter at a root of unity ϵ, whose order ℓ is odd. There is a quantum Frobenius morphism that embeds
be the specialisation of the latter at a root of unity ϵ, whose order ℓ is odd. There is a quantum Frobenius morphism that embeds 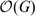 the function algebra of G, in
the function algebra of G, in 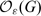 as a central Hopf subalgebra, so that
as a central Hopf subalgebra, so that 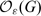 is a module over
is a module over 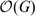 . When
. When 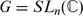 , it is known by [3], [4] that (the complexification of) such a module is free, with rank ℓdim(G). In this note we prove a PBW-like theorem for
, it is known by [3], [4] that (the complexification of) such a module is free, with rank ℓdim(G). In this note we prove a PBW-like theorem for 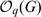 , and we show that – when G is Matn or GLn – it yields explicit bases of
, and we show that – when G is Matn or GLn – it yields explicit bases of 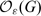 over
over 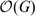 . As a direct application, we prove that
. As a direct application, we prove that 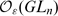 and
and 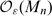 are free Frobenius extensions over
are free Frobenius extensions over 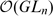 and
and 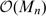 , thus extending some results of [5].
, thus extending some results of [5].

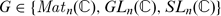 , let
, let 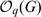 be the quantum function algebra – over
be the quantum function algebra – over 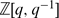 – associated to
– associated to 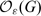 be the specialisation of the latter at a root of unity ϵ, whose order ℓ is odd. There is a quantum Frobenius morphism that embeds
be the specialisation of the latter at a root of unity ϵ, whose order ℓ is odd. There is a quantum Frobenius morphism that embeds 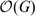 the function algebra of
the function algebra of 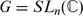 , it is known by [3], [4] that (the complexification of) such a module is free, with rank ℓ
, it is known by [3], [4] that (the complexification of) such a module is free, with rank ℓ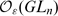 and
and 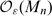 are free Frobenius extensions over
are free Frobenius extensions over 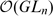 and
and 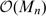 , thus extending some results of [5].
, thus extending some results of [5].