1 results
On the Pontrjagin Algebra of a Certain Class of Flags of Foliations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 1 / 01 March 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 77-83
- Print publication:
- 01 March 1985
-
- Article
-
- You have access
- Export citation
-
Let (𝓜,g) be a Riemannian manifold and let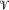
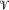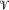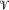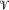1, 2, 3 be mutually orthogonal distributions on 𝓜 of dimensions p1, p2,P3 such that p1 + p2 + p3 = dim 𝓜. We assume that , and 1, ⊕ 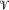2 are integrable and that all the geodesies of 𝓜 with initial tangent vector in 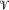2 remain tangent to 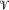2. Then, we prove that Pontk(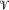2, ⊕ 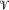3) = 0 for k > p2 + 2p3, where Pontk(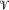2, ⊕ 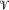3) is the subspace of the Pontrjagin algebra of 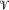2 ⊕ 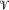3 generated by forms of degree k.
