For smooth functions 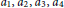 ${{a}_{1}}\,,\,{{a}_{2}}\,,\,{{a}_{3}}\,,\,{{a}_{4}}\,$ on a quaternion Heisenberg group, we characterize the existence of solutions of the partial differential operator system
${{a}_{1}}\,,\,{{a}_{2}}\,,\,{{a}_{3}}\,,\,{{a}_{4}}\,$ on a quaternion Heisenberg group, we characterize the existence of solutions of the partial differential operator system 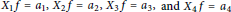 ${{X}_{1}}f\,=\,{{a}_{1}},\,{{X}_{2}}f=\,{{a}_{2}},\,{{X}_{3}}f\,=\,{{a}_{3}},\,\text{and}\,{{X}_{4}}f\,=\,{{a}_{4}}$. In addition, a formula for the solution function
${{X}_{1}}f\,=\,{{a}_{1}},\,{{X}_{2}}f=\,{{a}_{2}},\,{{X}_{3}}f\,=\,{{a}_{3}},\,\text{and}\,{{X}_{4}}f\,=\,{{a}_{4}}$. In addition, a formula for the solution function 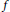 $f$ is deduced, assuming solvability of the system.
$f$ is deduced, assuming solvability of the system.