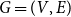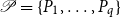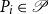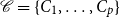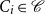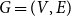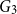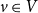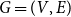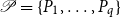Given a plane graph $G=(V,E)$ , a Petrie tour of G is a tour P of G that alternately turns left and right at each step. A Petrie tour partition of G is a collection ${\mathscr P}=\{P_1,\ldots,P_q\}$ of Petrie tours so that each edge of G is in exactly one tour 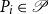$P_i \in {\mathscr P}$ . A Petrie tour P is called a Petrie cycle if all its vertices are distinct. 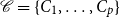A Petrie cycle partition of G is a collection ${\mathscr C}=\{C_1,\ldots,C_p\}$ of Petrie cycles so that each vertex of G is in exactly one cycle 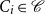$C_i \in {\mathscr C}$ . In this paper, we study the properties of 3-regular plane graphs that have Petrie cycle partitions and 4-regular plane multi-graphs that have Petrie tour partitions. 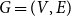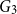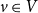Given a 4-regular plane multi-graph $G=(V,E)$ , a 3-regularization of G is a 3-regular plane graph $G_3$ obtained from G by splitting every vertex $v\in V$ into two degree-3 vertices. G is called Petrie partitionable if it has a 3-regularization that has a Petrie cycle partition. The general version of this problem is motivated by a data compression method, tristrip, used in computer graphics. In this paper, we present a simple characterization of Petrie partitionable graphs and show that the problem of determining if G is Petrie partitionable is NP-complete.