In response to an open problem raised by S. Rabinowitz, we prove that
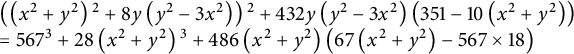 \begin{align*} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ =567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right) \end{array} \end{align*}
\begin{align*} \begin{array} [c]{l} \left( \left( x^{2}+y^{2}\right) {}^{2}+8y\left( y^{2}-3x^{2}\right) \right) {}^{2}+432y\left( y^{2}-3x^{2}\right) \left( 351-10\left( x^{2}+y^{2}\right) \right) \\ =567^{3}+28\left( x^{2}+y^{2}\right) {}^{3}+486\left( x^{2}+y^{2}\right) \left( 67\left( x^{2}+y^{2}\right) -567\times18\right) \end{array} \end{align*}
is the equation of a plane convex curve of constant width.