Search

O-minimal geometry generalizes both semialgebraic and subanalytic geometries, and has been very successful in solving special cases of some problems in arithmetic geometry, such as André–Oort conjecture. Among the many tools developed in an o-minimal setting are cohomology theories for abstract-definable continuous manifolds such as singular cohomology, sheaf cohomology and Čech cohomology, which have been used for instance to prove Pillay’s conjecture concerning definably compact groups. In the present thesis we elaborate an o-minimal de Rham cohomology theory for abst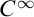ract-definable $C^{\infty }$ manifolds in an o-minimal expansion of the real field which admits smooth cell decomposition and defines the exponential function. We can specify the o-minimal cohomology groups and attain some properties such as the existence of Mayer–Vietoris sequence and the invariance under abstract-definable 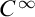$C^{\infty }$ diffeomorphisms. However, in order to obtain the invariance of our o-minimal cohomology under abstract-definable homotopy we must work in a tame context that defines sufficiently many primitives and assume the validity of a statement related to Bröcker’s question.