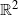We consider random rectangles in $\mathbb{R}^2$ that are distributed according to a Poisson random measure, i.e. independently and uniformly scattered in the plane. The distributions of the length and the width of the rectangles are heavy tailed with different parameters. We investigate the scaling behaviour of the related random fields as the intensity of the random measure grows to infinity while the mean edge lengths tend to zero. We characterise the arising scaling regimes, identify the limiting random fields, and give statistical properties of these limits.

A branching random field is considered as a model of either of two situations in genetics in which migration or dispersion plays a role. Specifically we consider the expected number of individuals NA in a (geographical) set A at time t, the covariance of NA and NB for two sets A, B, and the probability I(x, y, u) that two individuals found at locations x, y at time t are of the same genetic type if the population is subject to a selectively neutral mutation rate u. The last also leads to limit laws for the average degree of relationship of individuals in various types of branching random fields. We also find the equations that the mean and bivariate densities satisfy, and explicit formulas when the underlying migration process is Brownian motion.