We consider the 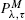 policy in a finite dam in which the input of water is formed by a compound Poisson process and the rate of water release is changed instantaneously from a to M and from M to a (M > a) at the moments when the level of water exceeds λ and downcrosses τ (λ > τ) respectively. After assigning costs to the changes of release rate, a reward to each unit of output, and a cost related to the level of water in the reservoir, we determine the long-run average cost per unit time.
policy in a finite dam in which the input of water is formed by a compound Poisson process and the rate of water release is changed instantaneously from a to M and from M to a (M > a) at the moments when the level of water exceeds λ and downcrosses τ (λ > τ) respectively. After assigning costs to the changes of release rate, a reward to each unit of output, and a cost related to the level of water in the reservoir, we determine the long-run average cost per unit time.