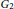1 results
Order 3 Elements in G2 and Idempotents in Symmetric Composition Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1075
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
-
Order three elements in the exceptional groups of type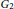
${{G}_{2}}$ are classified up to conjugation over arbitrary fields. Their centralizers are computed, and the associated classification of idempotents in symmetric composition algebras is obtained. Idempotents have played a key role in the study and classification of these algebras.Over an algebraically closed field, there are two conjugacy classes of order three elements in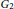
${{G}_{2}}$ in characteristic not 3 and four of them in characteristic 3. The centralizers in characteristic 3 fail to be smooth for one of these classes.
