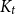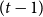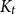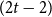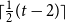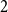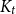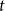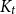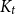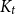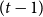Strengthening Hadwiger’s conjecture, Gerards and Seymour conjectured in 1995 that every graph with no odd $K_t$ -minor is properly $(t-1)$ -colourable. This is known as the Odd Hadwiger’s conjecture. We prove a relaxation of the above conjecture, namely we show that every graph with no odd 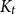$K_t$ -minor admits a vertex 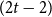$(2t-2)$ -colouring such that all monochromatic components have size at most 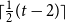$\lceil \frac{1}{2}(t-2) \rceil$ . The bound on the number of colours is optimal up to a factor of 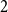$2$ , improves previous bounds for the same problem by Kawarabayashi (2008, Combin. Probab. Comput. 17 815–821), Kang and Oum (2019, Combin. Probab. Comput. 28 740–754), Liu and Wood (2021, arXiv preprint, arXiv:1905.09495), and strengthens a result by van den Heuvel and Wood (2018, J. Lond. Math. Soc. 98 129–148), who showed that the above conclusion holds under the more restrictive assumption that the graph is 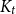$K_t$ -minor-free. In addition, the bound on the component-size in our result is much smaller than those of previous results, in which the dependency on 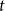$t$ was given by a function arising from the graph minor structure theorem of Robertson and Seymour. 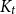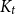Our short proof combines the method by van den Heuvel and Wood for $K_t$ -minor-free graphs with some additional ideas, which make the extension to odd $K_t$ -minor-free graphs possible.