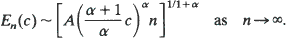We model a selection process arising in certain storage problems. A sequence (X1, · ··, Xn) of non-negative, independent and identically distributed random variables is given. F(x) denotes the common distribution of the Xi′s. With F(x) given we seek a decision rule for selecting a maximum number of the Xi′s subject to the following constraints: (1) the sum of the elements selected must not exceed a given constant c > 0, and (2) the Xi′s must be inspected in strict sequence with the decision to accept or reject an element being final at the time it is inspected.

We prove first that there exists such a rule of threshold type, i.e. the ith element inspected is accepted if and only if it is no larger than a threshold which depends only on i and the sum of the elements already accepted. Next, we prove that if F(x) ~ Axα as x → 0 for some A, α> 0, then for fixed c the expected number, En(c), selected by an optimal threshold is characterized by 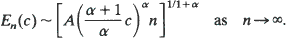Asymptotics as c → ∞and n → ∞with c/n held fixed are derived, and connections with several closely related, well-known problems are brought out and discussed.