1 results
Existence of a solution for a nonlinearly elastic plane membrane “under tension”
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 33 / Issue 5 / September 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1019-1032
- Print publication:
- September 1999
-
- Article
- Export citation
-
A justification of the two-dimensional nonlinear “membrane”equations for a plate made of a Saint Venant-Kirchhoff material hasbeen given by Fox et al. [9] by means of the method of formal asymptotic expansions applied to the three-dimensional equations of nonlinear elasticity. This model, which retains the material-frame indifference of the originalthree dimensional problem in the sense that its energy density isinvariant under the rotations of ${\mathbb{R}}^3$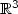
, is equivalent to finding thecritical points of a functional whose nonlinear part depends on the firstfundamental form of the unknown deformed surface. We establish here an existence result for these equations in the case of themembrane submitted to a boundary condition of “tension”, and we show that thesolution found in our analysis is injective and is the unique minimizer of thenonlinear membrane functional, which is not sequentially weakly lowersemi-continuous.We also analyze the behaviour of the membrane when the “tension” goes toinfinityand we conclude that a “well-extended” membrane may undergo largeloadings.
