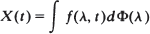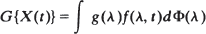We adapt the classical definition of locally stationary processes in discrete time (see e.g. Dahlhaus, ‘Locally stationary processes’, in Time Series Analysis: Methods and Applications (2012)) to the continuous-time setting and obtain equivalent representations in the time and frequency domains. From this, a unique time-varying spectral density is derived using the Wigner–Ville spectrum. As an example, we investigate time-varying Lévy-driven state space processes, including the class of time-varying Lévy-driven CARMA processes. First, the connection between these two classes of processes is examined. Considering a sequence of time-varying Lévy-driven state space processes, we then give sufficient conditions on the coefficient functions that ensure local stationarity with respect to the given definition.

A new method for obtaining spectral-like representations for a large class of non-stationary random processes is formulated. For a wide sense stationary process X(t) in continuous-time the spectral representation is generated by a self-adjoint operator H such that X(t)= eiHt X(0). Extending certain recently established operator identities for wide sense stationary processes, it is shown that similar operators exist for classes of non-stationary processes. The representation generated by such an operator has the form and it shares some of the properties of the wide sense stationary spectral representation: it is dual in a precisely defined sense to the time domain representation of X(t). There exists a class L of linear transformations of X(t) such that for G ∈ L for some function g determined by G.

We have introduced a definition of a slowly changing time-dependent linear transformation on a class of non-stationary stochastic processes and have studied the “spectral” relationship between the input and output processes. In addition, using this definition, we have extended one important property of coherency and the concept of residual variance bound pertinent to the theory of stationary stochastic processes to the non-stationary case.