1 results
Finite-dimensional approximations for Nica–Pimsner algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3375-3402
- Print publication:
- December 2020
-
- Article
- Export citation
-
We give necessary and sufficient conditions for nuclearity of Cuntz–Nica–Pimsner algebras for a variety of quasi-lattice ordered groups. First we deal with the free abelian lattice case. We use this as a stepping-stone to tackle product systems over quasi-lattices that are controlled by the free abelian lattice and satisfy a minimality property. Our setting accommodates examples like the Baumslag–Solitar lattice for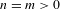
$n=m>0$ and the right-angled Artin groups. More generally, the class of quasi-lattices for which our results apply is closed under taking semi-direct and graph products. In the process we accomplish more. Our arguments tackle Nica–Pimsner algebras that admit a faithful conditional expectation on a small fixed point algebra and a faithful copy of the coefficient algebra. This is the case for CNP-relative quotients in-between the Toeplitz–Nica–Pimsner algebra and the Cuntz–Nica–Pimsner algebra. We complete this study with the relevant results on exactness.
